An Introduction To Probability For Gambling

Gambling can be a fun and interesting pass time if it doesn't ruin your life first. Today we will dive into how to win when gambling, by generating a statistical edge over the market or bookmakers.

The House Always Wins

The common saying goes: The house always wins. Why is that?

Let's play a simple game of chance, we will gamble on a coin flip. First let's assume we play naively, then I will show how we can win or lose. This game is simple:

You choose a side, and bet a dollar. If you're correct, you get two dollars (your original dollar, plus another dollar). If you're incorrect you lose your stake (one dollar).

Monte Carlo Simulations

Like in my article here we have created a random walk! But unlike our previous random walk, which sampled a normal distribution, in this case we can only go up or down by one (we either lose a dollar or gain a dollar), that's why it zig-zags around.

Expectation

Some of these random walks go up (winning), and some go down (losing), but we can decide whether we will be long term winners or long term losers by calculating the expected value:

$$\mathbb{E}[X] = \sum_{i=1}^n x_i \cdot P(X = x_i)$$ $$\mathbb{E}[X] = (1) \cdot \frac{1}{2} + (-1) \cdot \frac{1}{2} = 0$$

Our expected value is zero. This means if we play this gambling game for a long time, we will expect to neither win nor lose money.

The Overround And House Edge

How do casinos and bookmakers make money then? Well, an easy way to lose in our coin flip betting game, is to bet on odds less than fair value. We know that $odds=\frac{1}{prob}$, and for a fair coin flip, fair odds are: $\frac{1}{0.5}=2$.

Let's include an overround. An overround is the house edge, and it can range from only a few percent (sharp bookies) to more than 30%... think the slot machines.

The bookies would likely give us $1.80 on a fair coin flip... not very fair. Now let's return to our expected value calculation:

$$\mathbb{E}[X] = (1.80 - 1) \cdot \frac{1}{2} + (-1) \cdot \frac{1}{2}=-\frac{1}{10}$$

This means, for each dollar we bet, we expect to lose 10 cents. Let's run a monte carlo simulation with these odds:

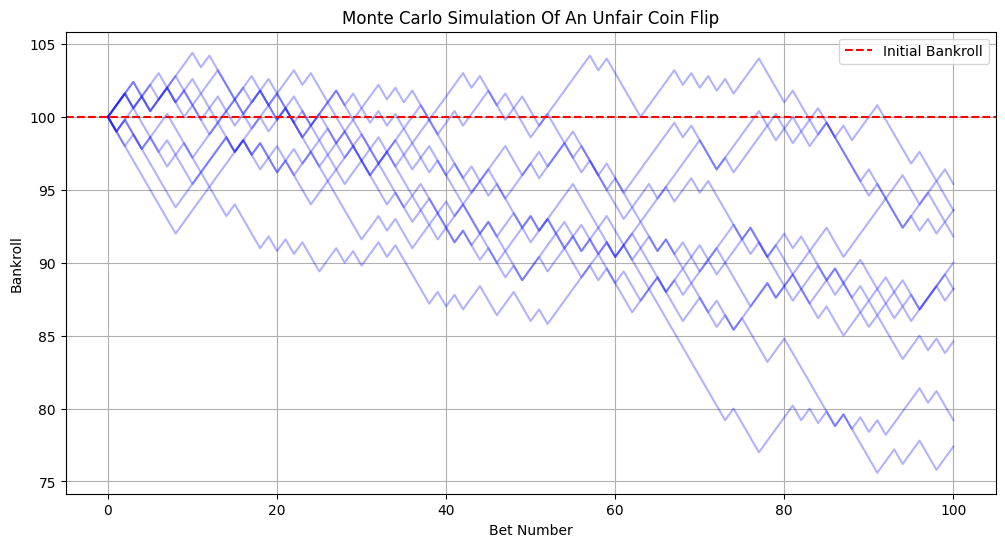
Note that for a bit, it even looks like we're winning, but eventually, we lose.

How To Consistently Make Money

We need to turn the statistics in our favour. This is the only way to make money from gambling, and it underpins all forms of profitable gambling, from the bookies themselves, to professionals like David Walsh and professional card counters.

Let's imagine we were able to agree on the odds of $2.20 with a bookmaker, we calculate our expected value, and re-run the simulation:

$$\mathbb{E}[X] = (2.20 - 1) \cdot \frac{1}{2} + (-1) \cdot \frac{1}{2}=\frac{1}{10}$$

This means for each 1$ bet, we will expect to profit 10 cents. Fantastic! Now let's re-run our simulation:

Slowly, we make money. It's hard graft and involves in this case placing hundreds of bets, in some cases we have still lost money after 100 bets, but statistically, we expect to win money.

Linear Growth

If I run our simulation again with more trials, we will notice a linear relationship:

That makes sense, because for each bet, we make 10 cents on the dollar, note that the gradient of the graph is approx $\frac{1}{10}$ which is expected as the positive rate of change. By staking instead a proportion of our bankroll (our total cash set aside for gambling), we can turn this graph into an exponential one:

Exponential Growth

Wow, now we're cooking with gas. This type of staking is called kelly staking, we we need to be careful here not to stake too much, or we risk financial ruin. Keep in mind, this only works if we have a positive expected value, otherwise we just multiply our losses (and our stupidity).

I hope this was an interesting and gentle introduction to the mathematics of gambling, in following articles, I will explain how we can put this theory to work in pricing betting markets.