Modelling Financial Markets With Random Walks

The Efficient Market Hypothesis

The efficient market hypothesis states that markets are efficient, meaning the current prices offered reflect all the available information known to the public at any given time. According to this hypothesis, financial markets do not exhibit easily identifiable trends which can be exploited to make money, this is because if there were such trends, someone would have start exploiting them to profit, and the trend would disappear.

Despite this, people do make money from trading and speculating on financial markets. In this article I will examine some of the mathematical properties which underpin financial markets in order to aid in our understanding of them.

The Price Ladder

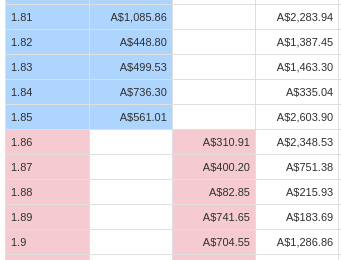
I am in particular interested in the betfair financial market, which allows people to bet on things with peers as opposed to a traditional bookmaker, offering and taking prices as you would on the ASX for example.

To simplify, I will pretend we are buying and selling an asset (in reality we are trading bets on things). The blue part is people that want to buy, and the corresponding orders they have placed, and the red part is people that want to sell, and the corresponding orders they have placed.

Note the sell price is always higher than the buy price, this makes sense, and becomes quite consequential, since if the buy price was larger than the sell price, a trade would take place and the seller would sell to the buyer.

Random Walks

When we look at the stock market, we see something like the image below. Sometimes it goes up, sometimes it goes down, sometimes it goes sideways.

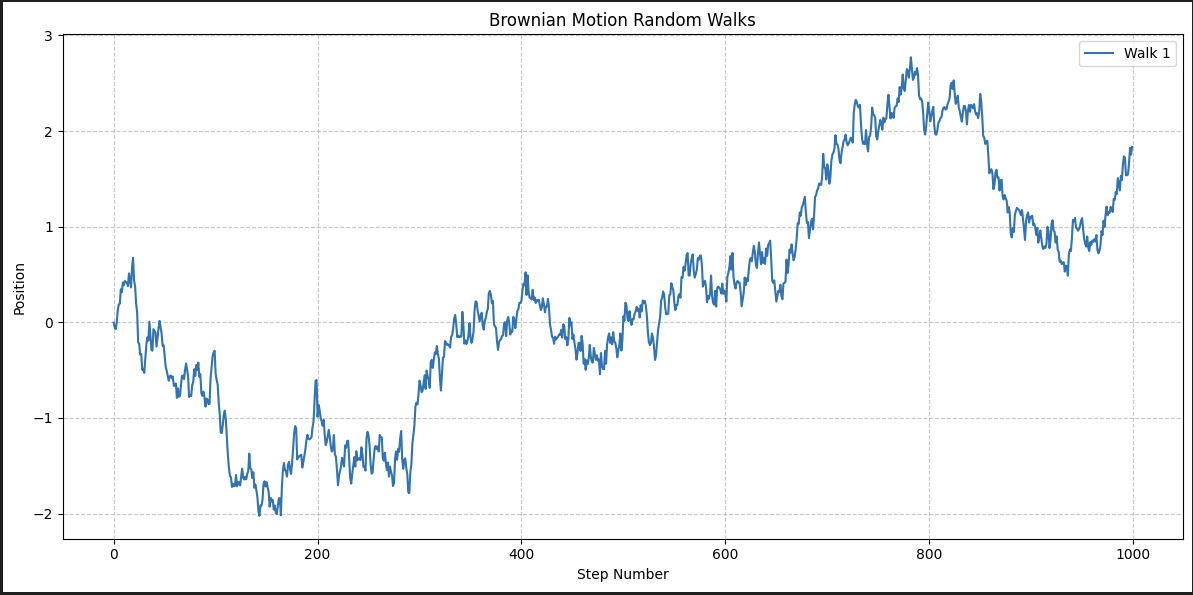
As per the efficient market hypothesis we saw before, we can't actually predict if it will go up or down based on this data alone, despite the temptation to. One might say, but look! There are periods when it goes up and keeps going up! Can't we just ride the trend? No.

Why? Because in this example I have generated this graph in a completely random way (using brownian motion), it is statistically guaranteed that there is absolutely no way to predict where the prices will go. Despite the fact that you can look back and identify retrospectively, what might look like trends, this is a correlation vs causation problem.

Let's look at the code used to generate the image above:

def brownian_walk(n_steps=1000, n_walks=5, step_size=0.1, seed=None):
    """
    Generate multiple random walks using Brownian motion.

    Parameters:
    - n_steps: Number of steps in each walk
    - n_walks: Number of independent random walks to generate
    - step_size: Standard deviation of the step distribution
    - seed: Random seed for reproducibility

    Returns:
    - walks: NumPy array of random walks
    """
    # Set random seed for reproducibility
    if seed is not None:
        np.random.seed(seed)

    # Generate random steps from a normal distribution
    # Steps are drawn from N(0, step_size)
    steps = np.random.normal(loc=0, scale=step_size, size=(n_walks, n_steps))

    # Compute cumulative sum to create walks
    # This converts incremental steps to cumulative position
    walks = np.cumsum(steps, axis=1)

    return walks

As you can see, the steps are sampled from a normal distribution. Sometimes they are big steps up, big steps down, or small steps that cause the current "price" to go in no particular direction.

Central Limit Theorem

If we now overlay many random walks on top of each other, we will see that we in fact will get a normal distribution:

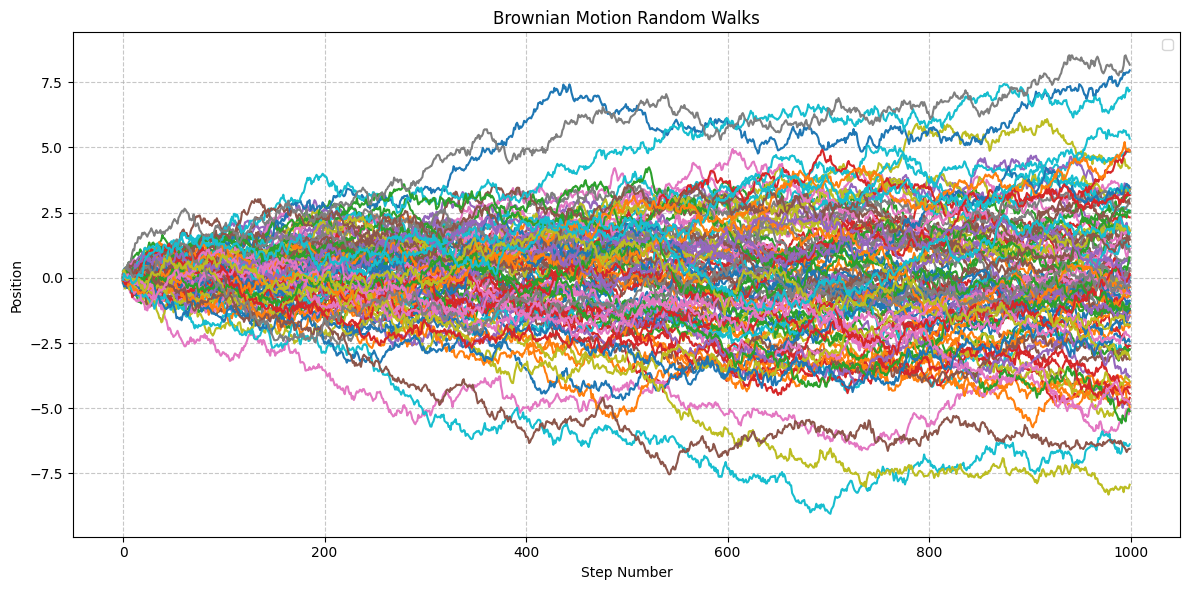
In this case, I have overlayed 100 random walks on each other. As you can see, there are a few that have gone either up or down by more than 7, and remarkably, it's symmetric! Why?

CLT! If I now plot the final values in a histogram, we will see what I mean:

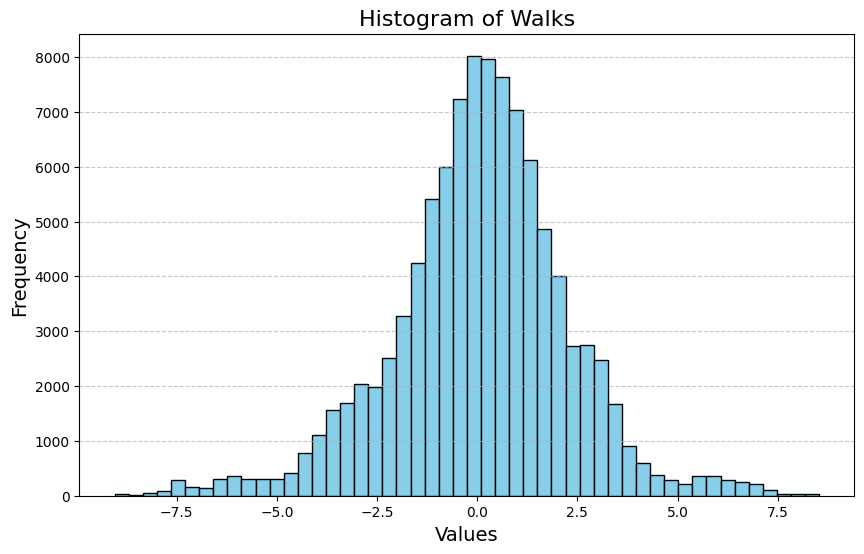
Well, that is not perfect, but it's close enough.

How Does This Relate To The Stock Market?

Clearly, if we can't predict where the prices are going based on past prices, we need strategies that will work regardless of where prices go in order to make money.

I will cover this in a later article so stay tuned...